Argmax流和多项式扩散:学习类别分布(flow部分未更新)
35th Conference on Neural Information Processing Systems (NeurIPS 2021).
生成流和扩散模型主要基于顺序数据(例如自然图像)进行训练。本文介绍了针对语言或图像分割等分类数据的流(flows)和扩散的两个扩展:Argmax流和多项式扩散。
- Argmax流由连续分布(如归一化流)和Argmax函数的组合定义。为了优化这个模型,我们学习了argmax的概率逆,它将分类数据提升到一个连续空间。
- 多项式扩散在扩散过程中逐渐增加类别噪声,为此学习生成去噪过程。
我们证明,我们的方法在文本建模和图像分割图建模方面的对数似然性优于现有的去量化方法
介绍
许多高维数据资源是分类别的,例如语言和图像分割。尽管大范围的自然图像是用生成流和扩散模型研究的,但可分类的数据并没有得到同样广泛的处理。目前,它们主要通过自回归模型进行建模,采样成本较高(Cooijmans等人,2017;Dai等人,2019)。
标准化流很有吸引力,因为它们可以被设计得在评估和采样方向都很快。通常,标准化流模拟连续分布。因此,直接优化离散数据流可能导致复杂度任意高。在文献中,通过在离散值周围的单位间隔中添加噪声,解决了有序数据的这一问题(Uria等人,2013;Theis等人,2016;Ho等人,2019)。然而,因为这些方法是为有序数据设计的,所以它们在分类数据上效果不佳。
另一种有吸引力的生成模型是扩散模型(Sohl Dickstein等人,2015),由于目标随着时间的推移而分解,因此训练速度很快(Ho等人,2020)。扩散模型通常具有逐渐增加噪声的固定扩散过程。这个过程由一个可学习的生成过程来补全,该过程对信号进行去噪(Song等人,2020);Nichol和Dhariwal(2021)表明,扩散模型也可以设计用于快速采样。到目前为止,扩散模型主要用于学习有序数据分布,如自然图像。
因此,在本文中,我们引入了可分类变量的流和扩散模型的扩展(如图1所示):
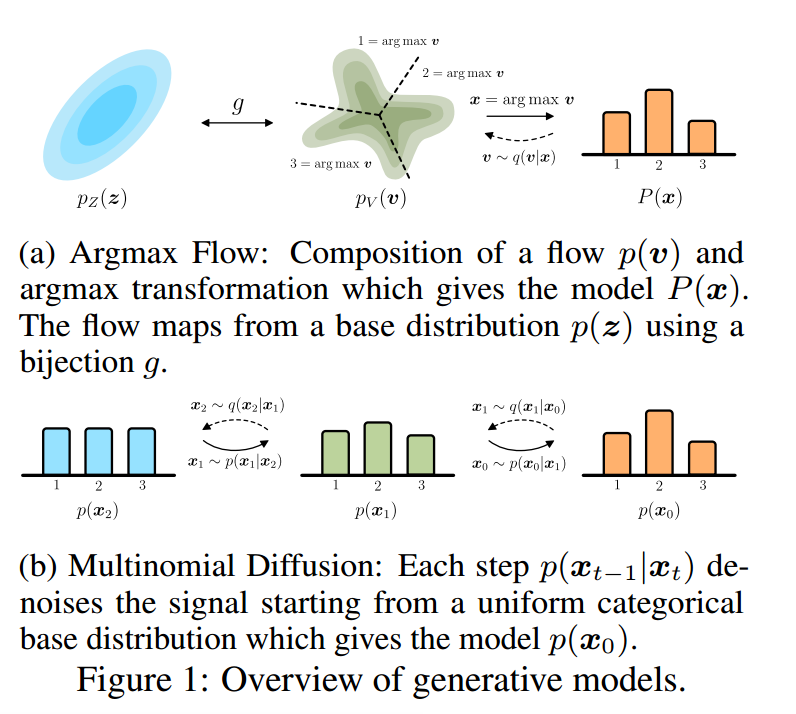
- Argmax流使用Argmax变换和Argmax的相应概率逆来弥合可分类数据和连续规范化流之间的差距。
- 我们引入了多项式扩散,这是一个直接定义在分类变量上的扩散模型。与标准化流相反,直接定义离散变量的扩散不需要梯度近似,因为扩散轨迹是固定的。
作为我们工作的结果,生成标准化流和扩散模型可以直接学习可分类数据。
背景
标准化流(暂时跳过)
扩散模型
给定数据\(x_0\),扩散模型(Sohl Dickstein等人,2015)由预定义的变分分布\(q(x_t | x_{t-1})\)组成,其在时间步长\(t \in\{1, …, T\}\)上逐渐增加噪声。扩散轨迹定义为\(q(x_t | x_{t-1})\)在\(x_{t-1}\)周围添加少量噪声。这样,信息逐渐被破坏,以至于在最后的时间步,\( x_T \)几乎不携带关于\(x_0\)的信息。它们生成的对应物,由学习去噪数据的可学习分布\(q(x_{t-1} | x_t)\)组成。当扩散过程增加足够少量的噪声时,其足以使用在维度轴上因子化(无相关性)的分布来定义去噪轨迹。分布\(p(x_T)\)被选择为类似于扩散轨迹所接近的分布。
可以使用变分推理优化扩散模型:
\( \mathcal{L} = \log p(x_0) \geq \mathbb{E}_{x_1,…,x_T \sim q} \left[ \log p(x_T) + \sum_{t=1}^T {\log \frac{p(x_{t-1} | x_t)}{q(x_t | x_{t-1})}} \right] \)
扩散中的一个重要见解是,通过对\(x_0\)进行条件处理,后验概率\( q(x_{t-1} | x_t, x_0 )= {q(x_t|x_{t-1})q(x_{t-1}|x_0)} / {q(x_t|x_0)} \) 易于处理且易于计算,从而允许根据具有较低方差的KL散度重新表述(Sohl Dickstein等人,2015)。注意,如果扩散轨迹\(q\)被很好地定义,则\( \mathrm{KL}(q(x_T\parallel x_0)|p(x_T)) \approx 0 \):
- 不等式3:
\( \mathcal{L} _{vb} = \log p(x_0) \geq \mathbb{E}_{q} \left[ \log p(x_0|x_1) – \mathrm{KL}(q(x_T|x_0)\parallel p(x_T)) – \sum_{t=2}^T { \mathrm{KL}(q(x_{t-1}|x_t,x_0)\parallel p(x_{t-1}|x_t)) } \right] \)
Argmax流(暂时跳过)
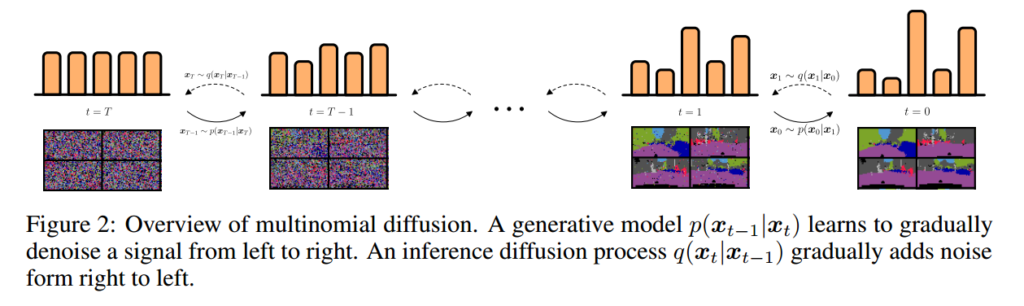
多项式扩散
在本节中,我们介绍了一种基于概率的分类数据模型:多项式扩散。与前面的部分不同,\(x_t\)将以一种one-hot编码格式\( x_t \in \left\{ 0,1 \right\} ^K\)表示。具体而言,对于类别\(k\),对于\(j \ne k\),有\( x_k = 1\)和\( x_j = 0 \)。注意为了清楚起见,再次省略了维度轴,因为所有分布都独立于维度轴。我们使用可分类的分布来定义多项式扩散过程,该分类分布有\( \beta _ t \)的机会均匀地重新采样一个类别:
- 等式11:
\( q(x_t|x_{t-1}) = \mathcal{C}(x_t|(1-\beta_t)x_{t-1} + \beta _t / K) \)
其中\( \mathcal{C} \)表示具有在|之后的概率参数的可分类的分布。标量和向量之间的进一步加法(和减法)是按元素进行的。这一惯例贯穿于本节。由于这些分布形成马尔可夫链,我们可以将给定\( x_0\)的任何\( x_t\)的概率表示为:
- 等式12:
\( q(x_t|x_0) = \mathcal{C}(x_t|\bar{\alpha} _t x_0 + (1-\bar{\alpha} _t)/ K) \)
其中\( \alpha _t=1-\beta _t \),\( \bar{\alpha} _t = \prod_{\tau = 1}^t{\alpha _\tau} \)。直观地,对于每个下一个时间步,\(K\)个类上引入少量均匀噪声\( \beta _t \),并且以大概率\( (1-\beta _t) \)对上一个值\( x_{t-1} \)进行采样。使用上述等式11和12,可以以封闭形式计算分类后验\(q(x_{t-1}|x_t,x0) \):
- 等式13:
\( q(x_{t-1}|x_t,x_0) = \mathcal{C}(x_{t-1}|\theta_{\mathrm{post}}(x_t,x_0)) \),其中\( \theta_{\mathrm{post}}(x_t,x_0)=\widetilde{\theta}/ \sum_{k=1}^K{\widetilde{\theta}_k} \)
同时\( \widetilde{\theta} = \left[ \alpha_t x_t + (1-\alpha_t)/K \right] \odot \left[ \bar{\alpha}_{t-1}x_0+(1-\bar{\alpha}_{t-1})/K \right] \)
Ho等人(2020)的一项创新是,他们没有直接预测生成轨迹的参数,而是使用\(q\)的后验方程来预测噪声。尽管预测离散数据的噪声是困难的,但我们从\(x_t\)预测\( \hat{x} _0 \)的概率向量,并随后使用概率向量\(q(x_{t-1}|x_t,\hat{x} _0) \)对\(p(x_{t-1}|x_t) \)进行参数化,其中\(x_0\)使用神经网络\( \hat{x} _0 = \mu(x_t,t)\)进行近似。方程13将产生非负的有效概率向量,并在预测\( \hat{x} _0\)为非负且和为1的条件下求和,这是通过\( \mu \)中的softmax函数确保的。总结如下:
- 等式14:
\( p(x_0|x_1) = \mathcal{C}(x_0|\hat{x} _0) \) 并且 \( p(x_{t-1}|x_t) = \mathcal{C}(x_{t-1}|\theta _{\mathrm{post}} (x_t,\hat{x} _0)) \)其中\( \hat{x} _0 = \mu (x_t,t) \)
不等式3中的KL项可以通过列举等式13和14中的概率并计算\(L_{t-1}\) ( \(t \geq 2\) )中离散分布的KL散度来简单地得出:
- 等式15:
\( \mathrm{KL}(q(x_{t-1}|x_t,x0)\parallel p(x_{t-1}|x_t)) = \mathrm{KL}(\mathcal{C}(\theta _{\mathrm{post}}(x_t,x_0))\parallel \mathcal{C}(\theta _\mathrm{post}(x_t,\hat{x} _0)))) \)
其可以使用\( \sum_{k} {\theta_{post}(x_t,x_0)_k \log \frac{\theta_{post} (x_t,x_0)_k}{\theta_{post} (x_t,\hat{x} _0)_k} }\)进行计算。此外,为了计算\( \log p (x_0|x_1)\),使用\(x_0\)是独热的:
- 等式16:
\( \log p (x_0|x_1) = \sum_{k} {x_{0,k} \log \hat{x}_{0,k}}\)
Multinomial Diffusion代码
GitHub – ehoogeboom/multinomial_diffusion
test